Antwoorden van 11-04-2025 (niveau 3F)
(klik op een pijltje om naar een andere datum te bladeren)
De deelnemers op niveau 3F hebben de test van 11-04-2025 zo ingevuld:

In een rekenboek uit 1910 worden lengtematen en inhoudsmaten ("ruimtematen") uitgelegd.
In die tijd was een Myriameter een gangbare term voor 10.000 meter.
Nu je dit weet, kun je ook berekenen:
1 kubieke Myriameter = ........ m³

1 Myriameter = 10 km = 10.000 m
1 kubieke Myriameter =
10.000 m x 10.000 m x 10.000 m =
1.000.000.000.000 m³ = 1 biljoen m³
Zie ook de pagina Meten en wegen.
Een feestganger ging na een avondje stappen op weg naar huis.
Onderweg kwam hij een arme man tegen, die hem om geld vroeg. Hij gaf hem de helft van al het geld dat hij nog op zak had, plus één euro extra.
Even later kwam hij een tweede arme man tegen en hij gaf hem de helft van het resterende geld plus twee euro extra.
En vlak voor zijn huis kwam hij een derde arme man tegen. Aan hem gaf hij de helft van het restant plus 3 euro.
Toen hij thuis was had hij nog maar één euro over.
Toen hij het café verliet, had hij ........ euro op zak.
(Vul alleen een getal in.)
(Een som van Hans Gunneweg.)
Je kunt het verhaal terugrekenen:
Bij de derde stop hield hij 1 euro over.
1 + 3 = 4 en 4 x 2 = 8
Bij de tweede stop hield hij 8 euro over.
8 + 2 = 10 en 2 x 10 = 20
Bij de eerste stop hield hij 20 euro over.
20 + 1 = 21 en 21 x 2 = 42.
Hij begon met 42 euro.
Of gebruik vergelijkingen:
Toen hij het café verliet, had hij nog a euro op zak.
Bij de eerste stop gaf hij a + 1 weg.
a + 1 weg.
Hij hield nog a - 1 over.
a - 1 over.
Bij de 2e stop gaf hij daarvan de helft + 2 euro weg:
 (
( a - 1) + 2, oftewel
a - 1) + 2, oftewel  a + 1
a + 1 .
.
Hij hield nog over:
 a - 1 - (
a - 1 - ( a + 1
a + 1 ).
).
Dat is a - 2
a - 2 .
.
Bij de derde stop gaf hij de helft daarvan + 3 weg. Dat is
 (
( a-
a-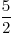 ) + 3 =
) + 3 =  a -
a -  + 3 =
+ 3 =  a + 1
a + 1
Hij hield hij nog over:
 a - 2
a - 2 - (
- ( a - 1
a - 1 ) =
) =  a - 4
a - 4 .
.
En dat was precies 1 euro.
 a - 4
a - 4 = 1
= 1
 a = 5
a = 5
a = 42
Controle:
Hij start met 42 euro.
Bij de eerste stop geeft hij 21 + 1 = 22 euro. Er blijft 20 euro over.
Bij de tweede stop geeft hij 10 + 2 = 12 euro. Er is nog 8 euro over.
Bij de derde stop geeft hij 4 + 3 = 7 euro. Er is nog 1 euro over.
Zie ook de pagina Gemengde bewerkingen.
Je kunt het verhaal terugrekenen:
Bij de derde stop hield hij 1 euro over.
1 + 3 = 4 en 4 x 2 = 8
Bij de tweede stop hield hij 8 euro over.
8 + 2 = 10 en 2 x 10 = 20
Bij de eerste stop hield hij 20 euro over.
20 + 1 = 21 en 21 x 2 = 42.
Hij begon met 42 euro.
Of gebruik vergelijkingen:
Toen hij het café verliet, had hij nog a euro op zak.
Bij de eerste stop gaf hij
 a + 1 weg.
a + 1 weg.Hij hield nog
 a - 1 over.
a - 1 over.Bij de 2e stop gaf hij daarvan de helft + 2 euro weg:
 (
( a - 1) + 2, oftewel
a - 1) + 2, oftewel  a + 1
a + 1 .
.Hij hield nog over:
 a - 1 - (
a - 1 - ( a + 1
a + 1 ).
).Dat is
 a - 2
a - 2 .
.Bij de derde stop gaf hij de helft daarvan + 3 weg. Dat is
 (
( a-
a-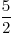 ) + 3 =
) + 3 =  a -
a -  + 3 =
+ 3 =  a + 1
a + 1
Hij hield hij nog over:
 a - 2
a - 2 - (
- ( a - 1
a - 1 ) =
) =  a - 4
a - 4 .
.En dat was precies 1 euro.
 a - 4
a - 4 = 1
= 1 a = 5
a = 5
a = 42
Controle:
Hij start met 42 euro.
Bij de eerste stop geeft hij 21 + 1 = 22 euro. Er blijft 20 euro over.
Bij de tweede stop geeft hij 10 + 2 = 12 euro. Er is nog 8 euro over.
Bij de derde stop geeft hij 4 + 3 = 7 euro. Er is nog 1 euro over.
Zie ook de pagina Gemengde bewerkingen.
TOTAALRESULTAAT:
Uitleg van de kleuren en symbolen:
Help | Contact | Instellingen |
Martin van Toll Producties
in samenwerking met

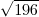 = ........
= ........ 