Voorbeeld 1: drie blokken

Je hebt drie blokken: rood, blauw en groen. 

Je stapelt de blokken op elkaar. Hoeveel verschillende volgordes zijn er mogelijk?

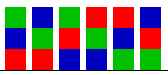
• Voor het onderste blok heb je 3 mogelijkheden: R, B, G.
• Als je het onderste blok geplaatst hebt, zijn er voor het middelste blok nog twee mogelijkheden.
• Als je dat blok geplaatst hebt, is er nog één kleur over voor het bovenste blok.
• Dat zijn 3 x 2 x 1 = 6 mogelijkheden. 

Of:

• Het rode blok kan op 3 plaatsen komen (onder, midden, boven).
• Daarna zijn er voor het blauwe blok nog twee posities over. 
• Daarna is er voor het groene blok nog één plaats over.
• Dat zijn 3 x 2 x 1 = 6 mogelijkheden. 

Voorbeeld 2: cijfercombinatie

Hoeveel combinaties van 4 verschillende cijfers kun je maken met de cijfers 0 t/m 9? 

• Voor het eerste cijfer bestaan 10 mogelijkheden (0 t/m 9).
• Omdat het getal uit verschillende cijfers moet bestaan, zijn er voor het tweede cijfer nog 9 mogelijkheden. 
• Voor het derde cijfer zijn er nog 8 mogelijkheden. 
• Voor het vierde cijfer zijn er 7 mogelijkheden. 
• In totaal zijn er 10 x 9 x 8 x 7 = 5040 combinaties van vier verschillende cijfers.

Voorbeeld 3: cijfercombinatie met extra voorwaarde.

Hoeveel getallen van 4 verschillende cijfers kun je maken met de cijfers 0 t/m 9? Extra voorwaarde: het getal mag niet met een 0 beginnen.

• Voor het eerste cijfer bestaan 9 mogelijkheden (1 t/m 9).
• Omdat het getal uit verschillende cijfers moet bestaan, zijn er voor het tweede cijfer nog 9 mogelijkheden (0 t/m 9, behalve het cijfer dat al op de eerste plaats staat).
• Voor het derde cijfer zijn er nog 8 mogelijkheden. 
• Voor het vierde cijfer zijn er 7 mogelijkheden. 
• In totaal zijn er 9 x 9 x 8 x 7 = 4536 getallen van vier verschillende cijfers.

Of: 

• Ga uit van voorbeeld 2 met 5040 combinaties. 
• Bij 10% van die combinaties staat een 0 op de eerste plaats. Die 504 combinaties mogen nu niet meedoen. 
• 5040 - 504 = 4536 getallen van vier verschillende cijfers.