|
0 actieve gebruikers Inloggen bestaande gebruiker Aanmelden nieuwe gebruiker Naar mobiele versie |
||||
 Merkwaardige producten
Merkwaardige productenIn de wiskunde bestaan enkele bijzondere vermenigvuldigingen die je vaak kunt tegenkomen bij het oplossen van sommen met vergelijkingen. Het is daarom handig als je zulke vermenigvuldigingen herkent. Zo'n bijzonder geval wordt een merkwaardig product genoemd. Hieronder staan een paar veel voorkomende merkwaardige producten.
- (a + b) x (a - b) = a² - b²
want:
(a + b) x (a - b) = a (a - b) + b (a - b) = a² - ab + ab - b² = a² - b²
of, getekend met vierkanten a² en b²: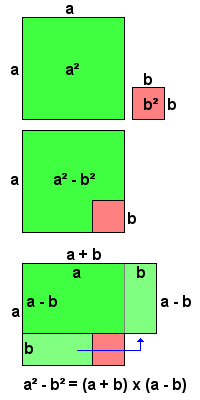
- (a + b)² = a² + 2ab + b²
want:
(a + b) x (a + b) = a (a + b) + b (a + b) = a² + ab + ab + b² = a² + 2ab + b²
of, getekend met vierkanten a² en b²: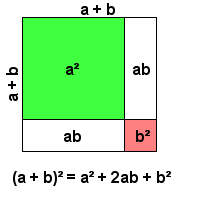
- (a - b)² = a² - 2ab + b²
want:
(a - b) x (a - b) = a (a - b) - b (a - b) = a² - ab - ab + b² = a² - 2ab + b²
of, getekend met vierkanten a² en b²: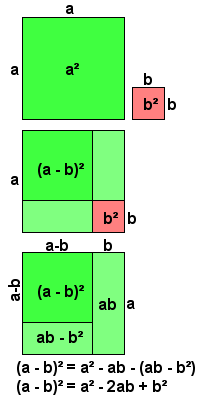
Een voorbeeldsom
Als je bij de leeftijd van een kind 4 optelt en daarvan het kwadraat neemt, zou het kind 16 keer zo oud zijn. Hoe oud is het kind?
In een vergelijking ziet dat er zo uit: (a + 4)² = a x 16
(a + 4) x (a + 4) = 16a
a x a + 4 x a + 4 x a + 4 x 4 = 16a
a² + 8a + 16 = 16a
a² - 8a + 16 = 0
hier herken je misschien 2b en b² van het merkwaardig product (a - b)²
(a - 4)² = 0
a - 4 = 0
a = 4
© 2010 - Beter Rekenen is een initiatief van |
